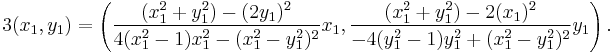Edwards curve
In mathematics, an Edwards curve is a new representation of elliptic curves, discovered by Harold M. Edwards in 2007. The concept of elliptic curves over finite fields is widely used in elliptic curve cryptography. Its applications to cryptography were developed by Bernstein and Lange: they pointed out several advantages of the Edwards form in comparison to the more well known Weierstrass form.
Contents |
Definition
The equation of an Edwards curve over a field K which does not have characteristic 2 is:
for some scalar 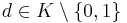 . Also the following form with parameters c and d is called an Edwards curve:
. Also the following form with parameters c and d is called an Edwards curve:
where c, d ∈ K with cd(1 − c4·d) ≠ 0.
Every Edwards curve is birationally equivalent to an elliptic curve in Weierstrass form. If K is finite, then a sizeable fraction of all elliptic curves over K can be written as Edwards curves. Often elliptic curves in Edwards form are defined having c=1, without loss of generality. In the following sections, it is assumed that c=1.
The group law
(See also Weierstrass curve group law)
It is possible to do some operations on the points on any elliptic curve, such as adding two or more points and doubling or tripling one. Usually, given two points P and Q on an elliptic curve, the point P + Q is directly related to third point of intersection between the curve and the line that passes trough P and Q; but in the case of Edwards curve this is not true: indeed the curve expressed in Edwards form has degree 4, so drawing a line one gets not 3 but 4 intersection points. For this case a geometric explanation of the addition law is given in [1]
Edwards addition law
It is possible to add points on an elliptic curve, and, in this way, obtain another point that belongs to the curve as well.
To understand better the concept of "addition" between points on a curve, a nice example is given by the circle:
take the circle of radius 1
and consider two points P1=(x1,y1), P2=(x2,y2) on it. Let α1 and α2 be the angles such that:
The sum of P1 and P2 is, thus, given by the sum of "their angles". That is, the point P3=P1+P2 is a point on the circle with coordinates (x3,y3), where:
In this way, the addition formula for points on the circle of radius 1 is:
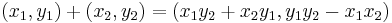 .
.
When two points (x1, y1) and (x2, y2) on an Edwards curve are added, the result is another point which has coordinates:
The neutral element of this addition is (0, 1). The inverse of any point (x1y1) is (−x1y1). The point (0, −1) has order 2: this means that the sum of this point to itself gives the "zero element" that is the neutral element of the group law, i.e. 2(0, −1) = (0, 1).
If d is not a square in K, then there are no exceptional points: the denominators 1 + dx1x2y1y2 and 1 − dx1x2y1y2 are always nonzero. Therefore, the Edwards addition law is complete when d is not a square in K. This means that the formulas work for all pairs of input points on the edward curve with no exceptions for doubling, no exception for the neutral element, no exception for negatives, etc.[2] In other words, it is defined for all pairs of input points on the Edwards curve over K and the result gives the sum of the input points.
If d is a square in K, then the same operation can have exceptional points, i.e. there can be pairs (x1, y1) and (x2, y2) where 1 + dx1x2y1y2 = 0 or 1 − dx1x2y1y2 = 0.
One of the attractive feature of the Edwards Addition law is that it is strongly unified i.e. it can also be used to double a point, simplifying protection against side-channel attack. The addition formula above is faster than other unified formulas and has the strong property of completeness[2]
Example of addition law :
Let's consider the elliptic curve in the Edwards form with d=2
and the point 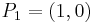 on it. It is possible to prove that the sum of P1 with the neutral element (0,1) gives again P1. Indeed, using the formula given above, the coordinates of the point given by this sum are:
on it. It is possible to prove that the sum of P1 with the neutral element (0,1) gives again P1. Indeed, using the formula given above, the coordinates of the point given by this sum are:
Projective homogeneous coordinates
In the context of cryptography, homogeneous coordinates are used to prevent field inversions that appear in the affine formula. To avoid inversions in the original Edwards addition formulas, the curve equation can be written in projective coordinates as:
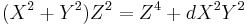 .
.
A projective point (X1 : Y1 : Z1) corresponds to the affine point (X1/Z1, Y1/Z1) on the Edwards curve.
The identity element is represented by (0 : 1 : 1). The inverse of (X1 : Y1 : Z1) is (−X1 : Y1 : Z1).
The addition formula in projective homogeneous coordinates is given by:
- (X3 : Y3 : Z3) = (X1 : Y1 : Z1) + (X2 : Y2 : Z2)
where
- X3 = Z1Z2(X1Y1 − Y1X2)(X1Y1Z222 + Z12X2Y2)
- Y3 = Z1Z2(X1X2 + Y1Y2)(X1Y1Z22 − Z12X2Y2)
- Z3 = kZ12Z22(X1X2 + Y1Y2)(X1Y2 − Y1X2) with k = 1/c.
Algorithm
Using the following algorithm, X3, Y3, Z3 can be written as: X3→ GJ , Y3→ HK, Z3→ kJK.d
where: A→ X1Z2,
B→ Y1Z2,
C→ Z1X2,
D→ Z1Y2,
E→ AB,
F→ CD,
G→ E+F,
H→ E-F,
J→ (A-C)(B+D)-H,
K→ (A+D)(B+C)-G
Doubling
Doubling can be performed with exactly the same formula as addition. Doubling refers to the case in which the inputs (x1, y1) and (x2, y2) are known to be equal. Since (x1, y1) is on the Edwards curve, one can substitute the coefficient by (x12 + y12 − 1)/x12y12 as follows:
This reduces the degree of the denominator from 4 to 2 which is reflected in faster doublings. A general addition in Edwards coordinates takes 10M + 1S + 1C + 1D + 7a and doubling costs 3M + 4S + 3C + 6a where M is field multiplications, S is field squarings, D is the cost of multiplying by a selectable curve parameter and a is field addition.
Example of doubling
As in the previous example for the addition law, let's consider the Edwards curve with d=2:
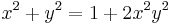
and the point P1=(1,0). The coordinates of the point 2P1 are:
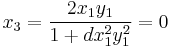
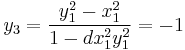
The point obtained from doubling P1 is thus P3=(0,-1).
Mixed Addition
Mixed addition is the case when Z2 is known to be 1. In such a case A=Z1.Z2 can be eliminated and the total cost reduces to 9M+1S+1C+1D+7a
Algorithm
A= Z1.Z2
B= ZI2
C=X1.X2
E=d.C.D
F=B-E
G=B+E
X3= Z1.F((XI+Y1).(X2+Y2)-C-D)
Y3= Z1.G.(D-C)
Z3=C.F.G
Tripling
Tripling can be done by first doubling the point and then adding the result to itself. By applying the curve equation as in doubling, we obtain
There are two sets of formulas for this operation in standard Edwards coordinates. The first one costs 9M + 4S while the second needs 7M + 7S. If the S/M ratio is very small, specifically below 2/3, then the second set is better while for larger ratios the first one is to be preferred.[3] Using the addition and doubling formulas (as mentioned above) the point (X1 : Y1 : Z1) is symbolically computed as 3(X1 : Y1 : Z1) and compared with (X3 : Y3 : Z3)
Example of tripling
Giving the Edwards curve with d=2, and the point P1=(1,0), the point 3P1 has coordinates:
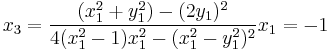
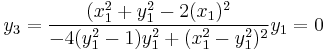
So, 3P1=(-1,0)=P-1. This result can also be found considering the doubling example: 2P1=(0,1), so 3P1 = 2P1 + P1 = (0,-1) + P1 = -P1.
Algorithm
A=X12
B=Y12
C=(2Z1)2
D=A+B
E=D2
F=2D.(A-B)
G=E-B.C
H=E-A.C
I=F+H
J=F-G
X3=G.J.X1
Y3=H.I.Y1
Z3=I.J.Z1
This formula costs 9M + 4S
Inverted Edwards coordinates
Bernstein and Lange introduced an even faster coordinate system for elliptic curves called the Inverted Edward coordinates[4] in which the coordinates (X : Y : Z) satisfy the curve (X2 + Y2)Z2 = (dZ4 + X2Y2) and corresponds to the affine point (Z/X, Z/Y) on the Edwards curve x2 + y2 = 1 + dx2y2 with XYZ ≠ 0.
Inverted Edwards coordinates, unlike standard Edwards coordinates, do not have complete addition formulas: some points, such as the neutral element, must be handled separately. But the addition formulas still have the advantage of strong unification: they can be used without change to double a point.
For more information about operations with these coordinates see http://hyperelliptic.org/EFD/g1p/auto-edwards-inverted.html
Extended Coordinates for Edward Curves
There is another coordinates system with which an Edwards curve can be represented; these new coordinates are called extended coordinates[5] and are even faster than inverted coordinates. For more information about the time-cost required in the operations with these coordinates see: http://hyperelliptic.org/EFD/g1p/auto-edwards.html
See also
For more information about the running-time required in a specific case, see Table of costs of operations in elliptic curves.
Notes
- ^ "Faster Computation of the Tate Pairing". 2009. http://eprint.iacr.org/2009/155. Retrieved 28 February 2010.
- ^ a b Daniel. J. Bernstein , Tanja Lange, pag. 3, Faster addition and doubling on elliptic curves
- ^ Bernstein et al., Optimizing Double-Base Elliptic curve single-scalar Multiplication
- ^ Daniel J.Bernstein . Tanja Lange , pag.2, Inverted Edward coordinates
- ^ H. Hisil, K. K. Wong, G. Carter, E. Dawson Faster group operations on elliptic curves
References
- Daniel Bernstein, T.Lange (2007), Faster Addition and Doubling on Elliptic curves, http://cr.yp.to/newelliptic/newelliptic-20070906.pdf
- Edwards, Harold M. (4/9/2007), "A normal form for elliptic curves", Bulletin of the American Mathematical Society (Providence, R.I.: American Mathematical Society) 44: 393–422, ISSN 0002-9904, http://www.ams.org/bull/2007-44-03/S0273-0979-07-01153-6/home.html, retrieved 2010/01/29
- Faster Group Operations on Elliptic curves, H. Hisil, K. K. Wong, G. Carter, E. Dawson
- D.J.Bernstein, P.Birkner. T. Lange, C.Peters, Optimizing Double-Base Elliptic-Curve Single-Scalar Multiplication, http://cr.yp.to/antiforgery/doublebase-20071028.pdf
- Washington, Lawrence C. (2008), Elliptic Curves: Number Theory and Cryptography, Discrete Mathematics and its Applications (2nd ed.), Chapman & Hall/CRC, ISBN 978-1-4200-7146-7
- Daniel J. Bernstein, T. Lange, Inverted Edwards coordinates, http://cr.yp.to/newelliptic/inverted-20071009.pdf
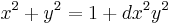
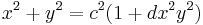
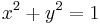
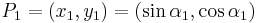
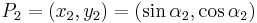
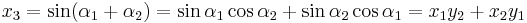
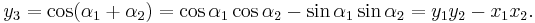
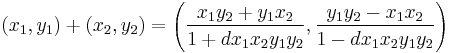
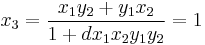
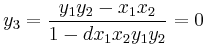
![\begin{align}
2(x_1,y_1) & = (x_1,y_1)%2B(x_1,y_1) \\[6pt]
2(x_1,y_1) & = \left( \frac{2x_1y_1}{1%2Bdx_1^2y_1^2}, \frac{y_1^2-x_1^2}{1-dx_1^2y_1^2} \right) \\[6pt]
& = \left( \frac{2x_1y_1}{x_1^2%2By_1^2}, \frac{y_1^2-x_1^2}{2-x_1^2-y_1^2} \right)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6c8344df75b4cce0eac4c8b0c3df3b45.png)